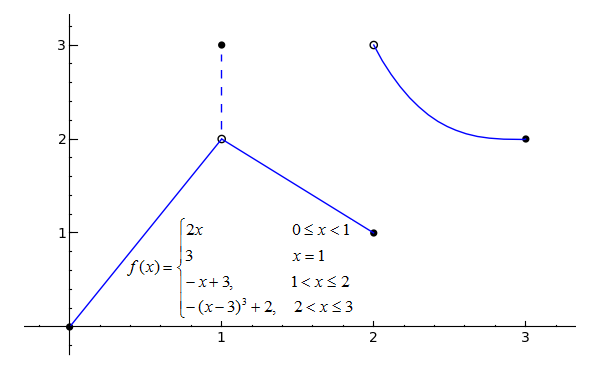
Describe the Continuity or Discontinuity of the Graphed Function

X1 x -6 Calculus - Discontinuity. We can see that this curve is smooth everywhere except at x-1.

Continuity Precalculus Ii

A continuous function can be graphed as a single connected curve.

. Fc is defined 2. If there is any break in the graph the function has a point of discontinuity. We have to graph this function and check which list of points lie on the graph.

A function is continuous when its graph is a single unbroken curve that you could draw without lifting your pen from the paper. The function graphed below is continuous everywhere. There are no sudden jumps and no missing values.

Calculus gives us a way to test for continuity using limits instead. So limit does not exist. The arrows on the function indicate it will grow infinitely large as x approaches a.

The function has a removable discontinuity at x 3. Go through the continuity and discontinuity examples given below. So this function is discontinuous at x3.

We know that sin x and cos x are the continuous function the product of sin x and cos x should also be a continuous function. X -1 x 6 C. So limit does not not exist.

Describe the continuity of the graphed function. 1 point O The function has a removable discontinuity at x 3. When graphed a removable discontinuity or a hole is just a missing value in the function.

The function has a nonremovable discontinuity at x 3. When is a function discontinuous. We can also talk about the continuity or discontinuity of functions.

The function graphed below is NOT continuous everywhere it is discontinuous at x 2 and. In this chapter well use graphs and formulas to describe continuity. Create graphs of three functions below to determine if they are continuous or discontinuous.

Since limit does not exists. The function has a nonremovable. The function is continuous.

When this happens we say the function has a jump discontinuity at xa. The function is approaching different values depending on the direction x is coming from. I was looking for the whole function however it only asked for which interval is the function increasing on.

We can see that left limit is not equal to right limit. We can see that this curve is smooth everywhere except at x3. The lim fx as x approaches c fc.

Discuss the continuity of the function fx sin x. Describe the continuity or discontinuity of the graphed function. A continuous function then moves toward each value in a predictable way and actually takes on that value.

I ii 3Tan2x1 iii 2 X1 Cos 3x each 2marks b Determine the discontinuities of the following functions and state why the function fails to be continuous at those points. Any function fx is continuous at xa only if. So we will check continuity at x-1.

Precalculus questions and answers. X 1 x6 D. If a function contains breaks that function isnt continuous.

The The function is continuous. Everything else looks like a continuous graph. If a function contains breaks that function isnt continuous.

A function is continuous if we can ensure arbitrarily small changes by restricting enough minor changes in its input. Calculus proves that a function is continuous when x a only under three conditions. Use the graph to answer the question also the one I put in the attachment.

Describe the continuity of the graphed function. Continuity and Discontinuity Examples. Since limit does not exist.

у 10 сл х 10 -10 -5 5 -5 -10 Use the graph to answer the question. So this function is discontinuous at x-1. Graphing functions can be tedious and for some functions impossible.

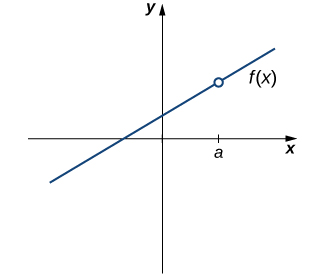
Take a screen shot of each save in a word document. The graph below shows a function that is discontinuous at xa. Find any points for the discontinuity for the rational function.

The function has an infinite discontinuity at x 3. The correct answer is B because it is increasing at points -10 and 10 or 1infinity. If the given function is not continuous then it is said to be discontinuous.

We can see that left limit is not equal to right limit. If we define that missing point we will have removed. If a function is not continuous at a point then we say it is discontinuous at that point.

The function has a removable discontinuity at x 0. Since square root is there we find that x can only be posiitve but y can be since square root both positive and negative. Continuous Function At the basic level teachers tend to describe continuous functions as those whose graphs.

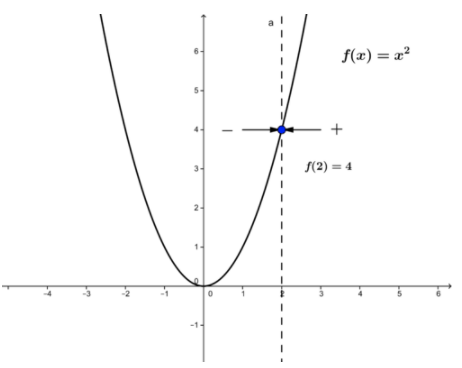
Learn about continuity in calculus and see examples of testing for continuity in both graphs and equations. The lim fx as x approaches c exists 3. When the function value and limit value are equal at the same point the function is described as continuous at that point.

So we will check continuity at x3. Continuity A function is a continuous at a point if its graph has no gaps holes breaks or jumps at that point. Any function fx is continuous at xa only if.

In mathematics a continuous function is a function that does not have discontinuities that means any unexpected changes in value. The function has a jump discontinuity at x 3. Without a graph to look at how can we determine if a function is continuous or not.

Discontinuity may be removable point infinite and jump with functions that fail at least one of the three conditions. I think the answer is D. More formally a function fx is continuous at a point c if.

Form A Graphing Continuity And Limits With Rational Functions Rational Function Ap Calculus Ap Calculus Ab

Sage Calculus Tutorial Continuity

Describe The Continuity Of The Graphed Function Brainly Com

Lots Of Points Urgent Describe The Continuity Or Discontinuity Of The Graphed Function Brainly Com

Continuity And Ivt

Describe The Continuity Of The Graphed Function Brainly Com

2 4 Continuity Calculus Volume 1

Expert Answer Describe The Continuity Of The Graphed Function Select All That Apply Brainly Com

3 1 Continuity Of A Function K12 Libretexts

Continuity And Discontinuity

Discontinuous Functions

Discontinuity In Math Definition And Types

Discontinuous Functions Removable Discontinuity Removable Discontinuity Occurs When The Limit Of The Function From The Left And Right Do Not Equal The Y Value When X Is Equal To The Given Value It Can Occur When One Point Is Separated From The Rest Of The

7 Continuous And Discontinuous Functions

Continuity And Ivt

Describe The Continuity Or Discontinuity Of The Graphed Function I Will Give More Points And Brainly Com

Describe The Continuity Of The Graphed Function Select All That Apply The Function Is Continuous Brainly Com

2 4 Continuity Calculus Volume 1

Describe The Continuity Of The Graphed Function Please Help Brainly Com